| 共轭梯度法在弹塑性模型数值实现中的应用 |
| |
| 作者姓名: | 代宁 耿大将 郭培军 周顺华 狄宏规 |
| |
| 作者单位: | 1.同济大学 道路与交通工程教育部重点实验室,上海 201804;2.同济大学 上海市轨道交通结构耐久与系统安全重点实验室,上海 201804;3.新城控股集团股份有限公司上海第二分公司,上海 201800;4.麦克马斯特大学 土木工程系, 汉密尔顿 L8S4L7 |
| |
| 基金项目: | 国家自然科学基金(51761135109);国家留学基金委项目(201906260113) |
| |
| 摘 要: | 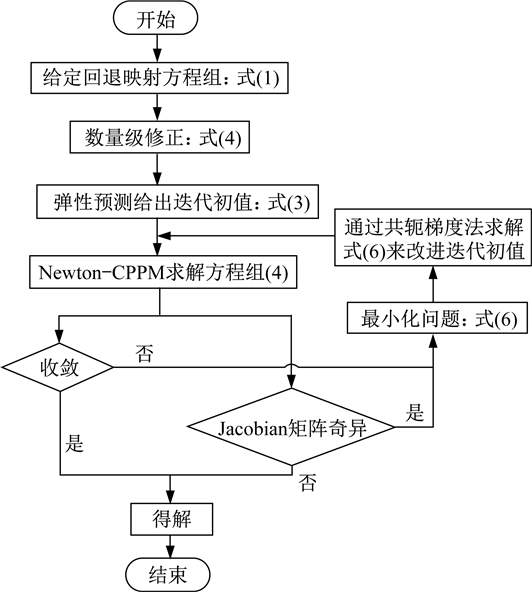
基于Jacobian矩阵的奇异和不收敛特性,分析了弹塑性本构模型的组成和算法。将牛顿?最近点投影法(Newton?CPPM)隐式算法中高度非线性方程组的求解问题转化为求最小值问题,通过采用共轭梯度法求解该最小值来实现对传统隐式算法的改进。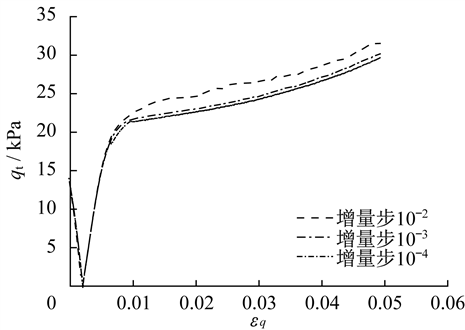
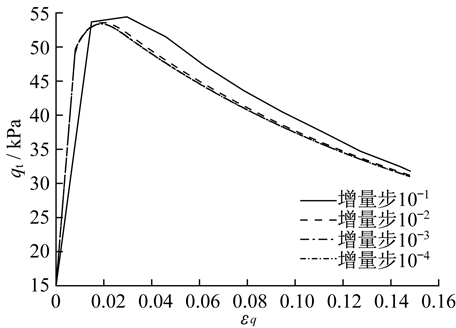
最后,以考虑软土结构性的Saniclay模型为例,在单元体分析计算的基础上,考虑不同的应变路径和初始应力状态,对传统隐式算法和改进隐式算法在计算收敛性、计算精度和计算效率方面进行对比,并通过工程算例检验传统隐式算法和改进隐式算法之间的差异。结果表明:相较于传统隐式算法,改进隐式算法能够有效提高计算效率和收敛性。
|
| 关 键 词: | 共轭梯度法 弹塑性本构模型 隐式算法 最小化 收敛性 |
| 收稿时间: | 2020-03-11 |
|
| 点击此处可从《同济大学学报(自然科学版)》浏览原始摘要信息 |
|
点击此处可从《同济大学学报(自然科学版)》下载免费的PDF全文 |
|



